blog posts and news stories

Revisiting The Relationship Between Internal and External Validity

The relationship between internal and external validity has been debated over the last few decades.

At the core of the debate is the question of whether causal validity comes before generalizability. To oversimplify this a bit, it is a question of whether knowing “what works” is logically prior to the question of what works “for whom and under what conditions.”

Some may consider the issue settled. I don’t count myself among them.

I think it is extremely important to revisit this question in the contemporary context, in which discussions are centering on issues of diversity of people and places, and the situatedness of programs and their effects.

In this blog I provide a new perspective on the issue, one that I hope rekindles the debate, and leads to productive new directions for research. (It builds on presentations at APPAM and SREE.)

I have organized the content into three degrees of depth. 1. For those interested in a perusal, I have addressed the main issues through a friendly dialogue presented below. 2. For those who want a deeper dive, I provide a video of a PowerPoint in which I take you through the steps of the argument. 3. The associated paper, Hold the Bets! Do Quasi-and True Experimental Evaluations Yield Equally Valid Impact Results When Effect Generalization is the Goal?, is currently posted as a preprint on SAGE Advance, and is under review by a journal.

Lastly, I would really value your comments to any of these works, to keep the conversation, and the progress in and beneficence from research going. Enjoy (and I hope to hear from you!),

Andrew Jaciw

The Great Place In-Between for Researchers and Evaluators

The impact evaluator is at an interesting crossroads between research and evaluation. There is an accompanying tension, but one that provides fodder for new ideas.

The perception of doing research, especially generalizable scientific research, is that it contributes information about the order of things, and about the relations among parts of systems in nature and society, that leads to cumulative and lasting knowledge.

Program evaluation is not quite the same. It addresses immediate needs, seldom has the luxury of time, and is meant to provide direction for critical stakeholders. It is governed by Program Evaluation Standards, of which Accuracy (including internal and statistical conclusions validity) is just one of many standards, with equal concern for Propriety and Stakeholder Representation.

The activities of the researcher and the evaluator may be seen as complementary, and the results of each can serve evaluative and scientific purposes.

The “impact evaluator” finds herself in a good place where the interests of the researcher-evaluator and evaluator-researcher overlap. This zone is a place where productive paradoxes emerge.

Here is an example from this zone. It takes the form of a friendly dialogue between an Evaluator-Researcher (ER) and a Researcher-Evaluator (RE).

ER: Being quizzical about the problem of external validity, I have proposed a novel method for answering the question of “what works”, or, more correctly of “what may work” in my context. It assumes a program has not yet been tried at my site of interest (the inference sample), and it involves comparing the performance across one or more sites where the program has been used, to performance at my site. The goal is to infer the impact for my site.

RE: Hold-on. So that’s kind of like a comparison group design but in reverse. You’re starting with an untreated group and comparing it to a treated group to draw an inference about potential impact for the untreated group. Right?

ER: Yes.

RE: But that does not make sense. That’s not the usual starting point. In research we start with the treated group and look for a valid control, not the other way around. I am confused.

ER: I understand, but when I was teaching, such comparisons were natural. For example, we compared the performance of a school just like ours, but that used Success For All (SFA), to performance at our school, which did not use SFA, to infer how we might have performed had we used the program. That is, to generalize the potential effect of the program for our site.

RE: You mean to predict impact for your site.

ER: Call it what you will. I prefer generalize because I am using information about performance under assignment to treatment from somewhere else.

RE: Hmmm. Odd, but OK (for now). However, why would you do that? Why not use an experimental result from somewhere else, maybe with some adjustment for differences in student composition and other things? You know, using reweighting methods, to produce a reasonable inference about potential impact for your site.

ER: I could, but that information would be coming from somewhere else where there are a lot of unknown variables about how that site operates, and I am not sure the local decision-makers would buy it. Coming from elsewhere it would be considered less-relevant.

RE: But your comparison also uses information from somewhere else. You’re using performance outcomes from somewhere else (where the treatment was implemented) to infer how your local site would have performed had the treatment been used there.

ER: Yes, but I am also preserving the true outcome in the absence of treatment (the ‘business as usual’ control outcome) for my site. I have half the true solution for my site. You’re asking me to get all my information from somewhere else.

RE: Yes, but I know the experimental result is unbiased from selection into conditions at the other “comparison” site, because of the randomized and uncompromised design. I‘ll take that over your “flipped” comparison group design any day!

ER: But your result may be biased from selection into sites, reflecting imbalance on known and possibly unknown moderators of impact. You’re talking about an experiment over there, and I have half the true solution over here, where I need it.

RE: I’ll take internal validity over there, first, and then worry about external validity to your site. Remember, internal validity is the “sine qua non”. Without it, you don’t have anything. Your approach seems deficient on two counts: first from lack of internal validity (you’re not using an experiment), and second from a lack of external validity (you’re drawing a comparison with somewhere else).

ER: OK, now you’re getting to the meat of things. Here is my bold conjecture: yes, internal and external validity bias both may be at play, but sometimes they may cancel each other out.

RE: What!? Like a chancy fluky kind of thing?

ER: No, systematically, and in principle.

RE: I don’t believe it. Two wrongs (biases) don’t make a right.

ER: But the product of two negatives makes a positive.

RE: I need something concrete to show what you mean.

ER: OK, here is an instance… The left vertical bar is the average impact for my site (site N). The right vertical bar is the average impact for the remote site (site M). The short horizontal bars show the values of Y (the outcome) for each site. (The black ones show values we can observe, the white-filled one shows an unobserved value [i.e., I don’t observe performance at my site (N) when treatment is provided, so the bar is empty.]) Bias1 is the difference between the other site and my site in the average impact (the difference in length of the vertical bars). Bias2 results from a comparison between sites in their average performance in the absence of treatment.

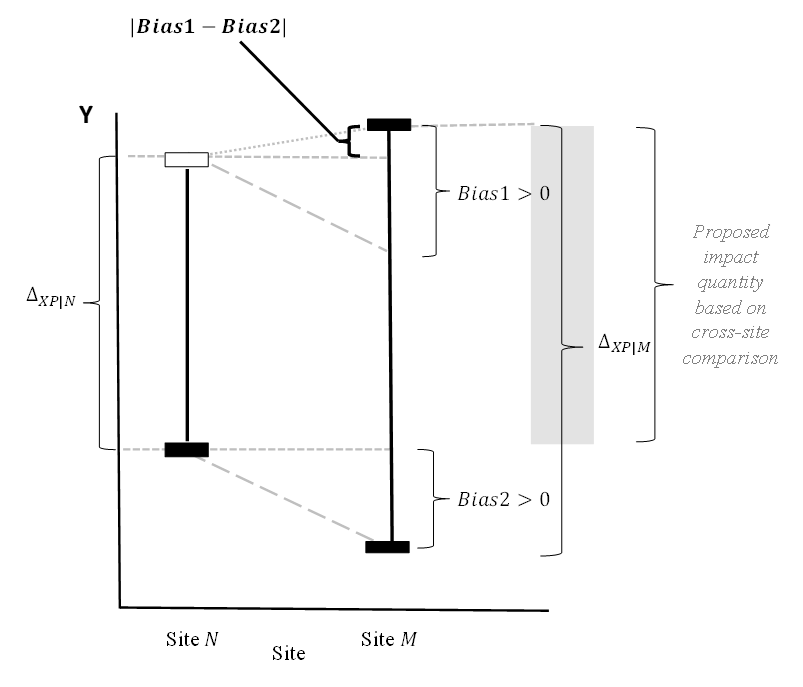
The point that matters here is that using the impact from the other site M (the length of the vertical line at M) to infer impact for my site N, leads to a result that is biased by an amount equal to the difference between the length of the vertical bars (Bias 1). But if I use the main approach that I am talking about, and compare performance under treatment at the remote site “M” (black bar at the top of Site M site) to the performance at my site without treatment (black bar at the bottom of Site N) the total bias is (Bias1 – Bias2), and the magnitude of this “net bias” is less than Bias1 by itself.

RE: Well, you have not figured-in the sampling error.

ER: Correct. We can do that, but for now let’s consider that we’re working with true values.

RE: OK, let’s say for the moment I accept what you’re saying. What does it do to the order and logic that internal validity precedes external validity?

ER: That is the question. What does it do? It seems that when generalizability is a concern, internal and external validity should be considered concurrently. Internal validity is the sole concern only when external validity is not at issue. You might say internal validity wins the race, but only when it’s the only runner.

RE: You’re going down a philosophical wormhole. That can be dangerous.

ER: Alright, then let’s stop here (for now).

RE and ER walk happily down the conference hall to the bar where RE has a double Jack, neat, and ER tries the house red.

BTW, here is the full argument and mathematical demonstration of the idea. Please share on social and tag us (our social handles are in the footer below). We’d love to know your thoughts. A.J.

Towards Greater (Local) Relevance of Causal Generalizations

To cite the paper we discuss in this blog post, use the reference below.

Jaciw, A. P., Unlu, F., & Nguyen, T. (2021). A within-study approach to evaluating the role of moderators of impact in limiting generalizations from “large to small”. American Journal of Evaluation. https://journals.sagepub.com/doi/10.1177/10982140211030552

Generalizability of Causal Inferences

The field of education has made much progress over the past 20 years in the use of rigorous methods, such as randomized experiments, for evaluating causal impacts of programs. This includes a growing number of studies on the generalizability of causal inferences stemming from the recognition of the prevalence of impact heterogeneity and its sources (Steiner et al., 2019). Most recent work on generalizability of causal inferences has focused on inferences from “small to large”. Studies typically include 30–70 schools while generalizations are made to inference populations at least ten times larger (Tipton et al., 2017). Such studies are typically used in informing decision makers concerned with impacts on broad scales, for example at the state level. However, as we are periodically reminded by the likes of Cronbach (1975, 1982) and Shadish et al. (2002), generalizations are of many types and support decisions on different levels. Causal inferences may be generalized not only to populations outside the study sample or to larger populations, but also to subgroups within the study sample and to smaller groups – even down to the individual! In practice, district and school officials who need local interpretations of the evidence might ask: “If a school reform effort demonstrates positive impact on some large scale, should I, as a principal, expect that the reform will have positive impact on the students in my school?” Our work introduces a new approach (or a new application of an old approach) to address questions of this type. We empirically evaluate how well causal inferences that are drawn on the large scale generalize to smaller scales.

The Research Method

We adapt a method from studies traditionally used (first in economics and then in education) to empirically measure the accuracy of program impact estimates from non-experiments. A central question is whether specific strategies result in better alignment between non-experimental impact findings and experimental benchmarks. Those studies—sometimes referred to as “Within-Study Comparison” studies (pioneered by Lalonde, 1986, and Fraker et al., 1987)—typically start with an estimate of a program’s impact from an uncompromised experiment. This result serves as the benchmark experimental impact finding. Then, to generate a non-experimental result, outcomes from the experimental control are replaced with those from a different comparison group. The difference in impact that results from this substitution measures the bias (inaccuracy) in the result that employs the non-experimental comparison. Researchers typically summarize this bias, and then try to remediate using various design and analysis-based strategies. (The Within-Study Comparison literature is vast and includes many studies that we cite in the article.)

Our Approach Follows a Within-Study Comparison Rationale and Method, but with a Focus on Generalizability.

We use data from the multisite Tennessee Student-Teacher Achievement Ratio (STAR) class size reduction experiment (described in Finn et al., 1990; Mosteller, 1995; Nye et al., 2000) to illustrate the application of our method. (We used 73 of the original 79 sites.) In the original study, students and teachers were randomized to small or regular-sized classes in grades K-3. Results showed a positive average impact of small classes. In our study, we ask whether a decisionmaker at a given site should accept this finding of an overall average positive impact as generalizable to his/her individual site.

We use the Within-Study Comparison Method as a Foundation.

First, we adopt the idea of using experimental benchmark impacts as the starting point. In the case of the STAR trial, each of the 73 individual sites yields its own benchmark value for impact. Second, consistent with Within-Study Comparisons, we select an alternative to compare against the benchmark. Specifically, we choose the average of impacts (the grand mean) across all sites as the generalized value. Third, we establish how closely this generalized value approximates impacts at individual sites (i.e., how well it generalizes “to the small”.) With STAR, we can do this 73 times, once for each site. Fourth, we summarize the discrepancies. Standard Within-Study Comparison methods typically average over the absolute values of individual biases. We adapt this, but instead use the average of 73 squared differences between the generalized impact and site-benchmark impacts. This allows us to capture the average discrepancy as a variance, specifically as the variation in impact across sites. We estimated this variation several ways, using alternative hierarchical linear models. Finally, we examine whether adjusting for imbalance between sites in site-level characteristics that potentially interact with treatment leads to closer alignment between the grand mean (generalized) and site-specific impacts. (Sometimes people wonder why, with Within-Study Comparison studies, if site-specific benchmark impacts are available, one would use less-optimal comparison group-based alternatives. With Within-Study Comparisons, the whole point is to see how closely we can replicate the benchmark quantity, in order to inform how well methods of causal inference (of generalization, in this case) potentially perform, in situations where we do not have an experimental benchmark.)

Our application is intentionally based on Within-Study Comparison methods. This is set out clearly in Jaciw (2010, 2016). Early applications with a similar approach can be found in Hotz, et al. (2005) and Hotz, et al. (2006). A new contribution of ours is that we summarize the discrepancy not as an average of absolute value of bias (a common metric in Within-Study Comparison studies), but as noted above, as a variance. This may sound like a nuanced technical detail, but we think it leads to an important interpretation: variation in impact is not just related to the problem of generalizability; rather, it directly indexes the accuracy (quantifies the degree of validity) of generalizations from “large to small”. We acknowledge Bloom et al. (2005) for the impetus for this idea, specifically, their insight that bias in Within-Study Comparison studies can be thought of as a type of “mismatch error”. Finally, we think it is important to acknowledge the ideas in G Theory from education (Cronbach et al., 1963; Shavelson et al., 2009). In that tradition, parsing variability in outcomes, accounting for its sources, and assessing the role of interactions among study factors, are central to the problem of generalizability.

Research Findings

First main result

The grand mean impact, on average, does not generalize reliably to the 73 sites. Before covariate adjustments, the average of the differences between the grand mean and the impacts at individual sites ranges between 0.41 and 0.25 standard deviations (SDs) of the outcome distribution, depending on the model used. After covariate adjustments, the average of the differences ranges between 0.41 and 0.17 SDs. (The average impact was about 0.25 SD.)

Second main result

Modeling effects of site-level covariates, and their interactions with treatment, only minimally reduced the between-site differences in impact.

The third main result

Whether impact heterogeneity achieves statistical significance depends on sampling error and correctly accounting for its sources. If we are going to provide accurate policy advice, we must make sure that we are not confusing random sampling error within sites (differences we would expect in results even if the program was not used) for variation in impact across sites. One source of random sampling error that is important but could be overlooked comes from classes. Given that teachers provide different value-added to students’ learning, we can expect differences in outcomes across classes. In STAR, with only a handful of teachers per school, the between-class differences easily add noise to the between-school outcomes and impacts. After adjusting for class random effects, the discrepancies in impact described above decreased by approximately 40%.

Research Conclusions

For the STAR experiment, the grand mean impact failed to generalize to individual sites. Adjusting for effects of moderators did not help much. Adjusting for class-level sampling error significantly reduced the level of measured heterogeneity. Even though the discrepancies decreased significantly after the class effects were included, the size of the discrepancies remained large enough to be substantively important, and therefore, we cannot conclude that the average impact generalized to individual sites.

In sum, based on this study, a policymaker at the site (school) level should apply caution in assessing whether the average result applies to his or her unique context.

The results remind us of an observation from Lee Cronbach (1982) about how a school board might best draw inferences about their local context serving a large Hispanic student body when program effects vary:

The school board might therefore do better to look at…small cities, cities with a large Hispanic minority, cities with well-trained teachers, and so on. Several interpretations-by-analogy can then be made….If these several conclusions are not too discordant, the board can have some confidence in the decision that it makes about its small city with well-trained teachers and a Hispanic clientele. When results in the various slices of data are dissimilar, it is better to try to understand the variation than to take the well-determined – but only remotely relevant – national average as the best available information. The school board cannot regard that average as superior information unless it believes that district characteristics do not matter (p. 167).

Some Possible Extensions of The Work

We’re looking forward to doing more work to continue to understand how to produce useful generalizations that support decision-making on smaller scales. Traditional Within-Study Comparison studies give us much food for thought, including about other designs and analysis strategies for inferring impacts to individual sites, and how to best communicate the discrepancies we observe and whether they are substantively large enough to matter for informing policy decisions and outcomes. One area of main interest concerns the quality of the moderators themselves; that is, how well they account for or explain impact heterogeneity. Here our approach diverges from traditional Within-Study Comparison studies. When applied to problems of internal validity, confounders can be seen as nuisances that make our impact estimates inaccurate. With regard to external validity, factors that interact with the treatment, and thereby produce variation in impact that affects generalizability, are not a nuisance; rather, they are an important source of information that may help us to understand the mechanisms through which the variation in impact occurs. Therefore, understanding the mechanisms relating the person, the program, context, and the outcome is key.

Lee Cronbach described the bounty of and interrelations among interactions in the social sciences as a “hall of mirrors”. We’re looking forward to continuing the careful journey along that hall to incrementally make sense of a complex world!

References

Bloom, H. S., Michalopoulos, C., & Hill, C. J. (2005). Using experiments to assess nonexperimental comparison -group methods for measuring program effect. In H. S. Bloom (Ed.), Learning more from social experiments (pp. 173 –235). Russell Sage Foundation.

Cronbach, L. J. (1975). Beyond the two disciplines of scientific psychology. American Psychologist, 30(2), 116–127.

Cronbach, L.J., Rajaratnam, N., & Gleser, G.C. (1963). Theory of generalizability: A liberation of reliability theory. The British Journal of Statistical Psychology, 16, 137-163.

Cronbach, L. J. (1982). Designing Evaluations of Educational and Social Programs. Jossey-Bass.

Finn, J. D., & Achilles, C. M., (1990). Answers and questions about class size: A statewide experiment. American Educational Research Journal, 27, 557-577.

Fraker, T., & Maynard, R. (1987). The adequacy of comparison group designs for evaluations of employment-related programs. The Journal of Human Resources, 22, 194–227.

Jaciw, A. P. (2010). Challenges to drawing generalized causal inferences in educational research: Methodological and philosophical considerations. [Doctoral dissertation, Stanford University.]

Jaciw, A. P. (2016). Assessing the accuracy of generalized inferences from comparison group studies using a within-study comparison approach: The methodology. Evaluation Review, 40, 199-240. https://journals.sagepub.com/doi/abs/10.1177/0193841x16664456

Hotz, V. J., Imbens, G. W., & Klerman, J. A. (2006). Evaluating the differential effects of alternative welfare-to-work training components: A reanalysis of the California GAIN Program. Journal of Labor Economics, 24, 521–566.

Hotz, V. J., Imbens, G. W. & Mortimer, J. H (2005). Predicting the efficacy of future training programs using past experiences at other locations. Journal of Econometrics, 125, 241–270.

Lalonde, R. (1986). Evaluating the econometric evaluations of training programs with experimental data. The American Economic Review, 76, 604–620.

Mosteller, F., (1995). The Tennessee study of class size in the early school grades. The Future of Children, 5, 113-127.

Nye, B., Hedges, L. V., & Konstantopoulos, (2000). The effects of small classes on academic achievement: The results of the Tennessee class size experiment. American Educational Research Journal, 37, 123-151.

Fraker, T., & Maynard, R. (1987). The adequacy of comparison group designs for evaluations of employment-related programs. The Journal of Human Resources, 22, 194–227.

Shadish, W. R., Cook, T. D., & Campbell, D. T., (2002). Experimental and Quasi-experimental Designs for Generalized Causal Inference. Houghton Mifflin.

Shavelson, R. J., & Webb, N. M. (2009). Generalizability theory and its contributions to the discussion of the generalizability of research findings. In K. Ercikan & W. M. Roth (Eds.), Generalizing from educational research (pp. 13–32). Routledge.

Steiner, P. M., Wong, V. C. & Anglin, K. (2019). A causal replication framework for designing and assessing replication efforts. Zeitschrift fur Psychologie, 227, 280–292.

Tipton, E., Hallberg, K., Hedges, L. V., & Chan, W. (2017). Implications of small samples for generalization: Adjustments and rules of thumb. Evaluation Review, 41(5), 472–505.

Jaciw, A. P., Unlu, F., & Nguyen, T. (2021). A within-study approach to evaluating the role of moderators of impact in limiting generalizations from “large to small”. American Journal of Evaluation. https://journals.sagepub.com/doi/10.1177/10982140211030552

^{Photo by drmakete lab}

Introducing SEERNet with the Goal of Replication Research

In 2021, we partnered with Digital Promise on a research proposal for the IES research network: Digital Learning Platforms to Enable Efficient Education Research Network. The project, SEER Research Network for Digital Learning Platforms (SEERNet) was funded through an IES education research grant in fall 2021, and we took off running. Digital Promise launched this SEERNet website to keep the community up to date on our progress. We’ve been meeting with five platform hosts, selected by IES, to develop ideas for replication research, generalizability in research, and rapid research.

The goal of SEERNet is to integrate rigorous education research into existing digital learning platforms (DLPs) in an effort to modernize research. The digital learning platforms have the potential to support education researchers as they study new ideas and seek to replicate those ideas quickly, across many sites, with a wide range of student populations and with a variety of education research topics. Each of the five platforms (listed below) will eventually have over 100,000 users, allowing us to explore ways to increase the efficiency of a replication study.

1. Kinetic by OpenStax
2. UpGrade/MATHia by Carnegie Learning
3. Learning at Scale by Arizona State University
4. E-Trials by ASSISTments
5. Terracotta by Canvas

As the network leads, Empirical Education and Digital Promise will work to share best practices among the DLPs and build a community of researchers and practitioners interested in the opportunities afforded by these innovative platforms for impactful research. Stay tuned for more updates on how you can get involved!

^{This project is supported by the Institute of Education Sciences, U.S. Department of Education, through Grant R305N210034 to Digital Promise. The opinions expressed are those of the authors and do not represent views of the Institute or the U.S. Department of Education.}

How Efficacy Studies Can Help Decision-makers Decide if a Product is Likely to Work in Their Schools

We and our colleagues have been working on translating the results of rigorous studies of the impact of educational products, programs, and policies for people in school districts who are making the decisions whether to purchase or even just try out—pilot—the product. We are influenced by Stanford University Methodologist Lee Cronbach, especially his seminal book (1982) and article (1975) where he concludes “When we give proper weight to local conditions, any generalization is a working hypothesis, not a conclusion…positive results obtained with a new procedure for early education in one community warrant another community trying it. But instead of trusting that those results generalize, the next community needs its own local evaluation” (p. 125). In other words, we consider even the best designed experiment to be like a case study, as much about the local and moderating role of context, as about the treatment when interpreting the causal effect of the program.

Following the focus on context, we can consider characteristics of the people and of the institution where the experiment was conducted to be co-causes of the result that deserve full attention—even though, technically, only the treatment, which was randomly assigned was controlled. Here we argue that any generalization from a rigorous study, where the question is whether the product is likely to be worth trying in a new district, must consider the full context of the study.

Technically, in the language of evaluation research, these differences in who or where the product or “treatment” works are called “interaction effects” between the treatment and the characteristic of interest (e.g., subgroups of students by demographic category or achievement level, teachers with different skills, or bandwidth available in the building). The characteristic of interest can be called a “moderator”, since it changes, or moderates, the impact of the treatment. An interaction reveals if there is differential impact and whether a group with a particular characteristic is advantaged, disadvantaged, or unaffected by the product.

The rules set out by The Department of Education’s What Works Clearinghouse (WWC) focus on the validity of the experimental conclusion: Did the program work on average compared to a control group? Whether it works better for poor kids than for middle class kids, works better for uncertified teachers versus veteran teachers, increases or closes a gap between English learners and those who are proficient, are not part of the information provided in their reviews. But these differences are exactly what buyers need in order to understand whether the product is a good candidate for a population like theirs. If a program works substantially better for English proficient students than for English learners, and the purchasing school has largely the latter type of student, it is important that the school administrator know the context for the research and the result.

The accuracy of an experimental finding depends on it not being moderated by conditions. This is recognized with recent methods of generalization (Tipton, 2013) that essentially apply non-experimental adjustments to experimental results to make them more accurate and more relevant to specific local contexts.

Work by Jaciw (2016a, 2016b) takes this one step further.

First, he confirms the result that if the impact of the program is moderated, and if moderators are distributed differently between sites, then an experimental result from one site will yield a biased inference for another site. This would be the case, for example, if the impact of a program depends on individual socioeconomic status, and there is a difference between the study and inference sites in the proportion of individuals with low socioeconomic status. Conditions for this “external validity bias” are well understood, but the consequences are addressed much less often than the usual selection bias. Experiments can yield accurate results about the efficacy of a program for the sample studied, but that average may not apply either to a subgroup within the sample or to a population outside the study.

Second, he uses results from a multisite trial to show empirically that there is potential for significant bias when inferring experimental results from one subset of sites to other inference sites within the study; however, moderators can account for much of the variation in impact across sites. Average impact findings from experiments provide a summary of whether a program works, but leaves the consumer guessing about the boundary conditions for that effect—the limits beyond which the average effect ceases to apply. Cronbach was highly aware of this, titling a chapter in his 1982 book “The Limited Reach of Internal Validity”. Using terms like “unbiased” to describe impact findings from experiments is correct in a technical sense (i.e., the point estimate, on hypothetical repeated sampling, is centered on the true average effect for the sample studied), but it can impart an incorrect sense of the external validity of the result: that it applies beyond the instance of the study.

Implications of the work cited, are, first, that it is possible to unpack marginal impact estimates through subgroup and moderator analyses to arrive at more-accurate inferences for individuals. Second, that we should do so—why obscure differences by paying attention to only the grand mean impact estimate for the sample? And third, that we should be planful in deciding which subgroups to assess impacts for in the context of individual experiments.

Local decision-makers’ primary concern should be with whether a program will work with their specific population, and to ask for causal evidence that considers local conditions through the moderating role of student, teacher, and school attributes. Looking at finer differences in impact may elicit criticism that it introduces another type of uncertainty—specifically from random sampling error—which may be minimal with gross impacts and large samples, but influential when looking at differences in impact with more and smaller samples. This is a fair criticism, but differential effects may be less susceptible to random perturbations (low power) than assumed, especially if subgroups are identified at individual levels in the context of cluster randomized trials (e.g., individual student-level SES, as opposed to school average SES) (Bloom, 2005; Jaciw, Lin, & Ma, 2016).

References:
Bloom, H. S. (2005). Randomizing groups to evaluate place-based programs. In H. S. Bloom (Ed.), Learning more from social experiments. New York: Russell Sage Foundation.

Cronbach, L. J. (1975). Beyond the two disciplines of scientific psychology. American Psychologist, 116-127.

Cronbach, L. J. (1982). Designing evaluations of educational and social programs. San Francisco, CA: Jossey-Bass.

Jaciw, A. P. (2016). Applications of a within-study comparison approach for evaluating bias in generalized causal inferences from comparison group studies. Evaluation Review, (40)3, 241-276. Retrieved from https://journals.sagepub.com/doi/abs/10.1177/0193841X16664457

Jaciw, A. P. (2016). Assessing the accuracy of generalized inferences from comparison group studies using a within-study comparison approach: The methodology. Evaluation Review, (40)3, 199-240. Retrieved from https://journals.sagepub.com/doi/abs/10.1177/0193841x16664456

Jaciw, A., Lin, L., & Ma, B. (2016). An empirical study of design parameters for assessing differential impacts for students in group randomized trials. Evaluation Review. Retrieved from https://journals.sagepub.com/doi/10.1177/0193841X16659600

Tipton, E. (2013). Improving generalizations from experiments using propensity score subclassification: Assumptions, properties, and contexts. Journal of Educational and Behavioral Statistics, 38, 239-266.

APPAM doesn’t stand for A Pretty Pithy Abbreviated Meeting

APPAM does stand for excellence, critical thinking, and quality research.

The 2017 fall research conference kept reminding me of one recurrent theme: bridging the chasms between researchers, policymakers, and practitioners.

Linear processes don’t work. Participatory research is critical!

Another hot topic is generalizability! There is a lot of work to be done here. What works? For whom? Why?

Lots of food for thought!

The Value of Looking at Local Results

The report we released today has an interesting history that shows the value of looking beyond the initial results of an experiment. Later this week, we are presenting a paper at AERA entitled “In School Settings, Are All RCTs Exploratory?” The findings we report from our experiment with an iPad application were part of the inspiration for this. If Riverside Unified had not looked at its own data, we would not, in the normal course of data analysis, have broken the results out by individual districts, and our conclusion would have been that there was no discernible impact of the app. We can cite many other cases where looking at subgroups leads us to conclusions different from the conclusion based on the result averaged across the whole sample. Our report on AMSTI is another case we will cite in our AERA paper.

We agree with the Institute of Education Sciences (IES) in taking a disciplined approach in requiring that researchers “call their shots” by naming the small number of outcomes considered most important in any experiment. All other questions are fine to look at but fall into the category of exploratory work. What we want to guard against, however, is the implication that answers to primary questions, which often are concerned with average impacts for the study sample as a whole, must apply to various subgroups within the sample, and therefore can be broadly generalized by practitioners, developers, and policy makers.

If we find an average impact but in exploratory analysis discover plausible, policy-relevant, and statistically strong differential effects for subgroups, then some doubt about completeness may be cast on the value of the confirmatory finding. We may not be certain of a moderator effect—for example—but once it comes to light, the value of the average impact can also be considered incomplete or misleading for practical purposes. If it is necessary to conduct an additional experiment to verify a differential subgroup impact, the same experiment may verify that the average impact is not what practitioners, developers, and policy makers should be concerned with.

In our paper at AERA, we are proposing that any result from a school-based experiment should be treated as provisional by practitioners, developers, and policy makers. The results of RCTs can be very useful, but the challenges of generalizability of the results from even the most stringently designed experiment mean that the results should be considered the basis for a hypothesis that the intervention may work under similar conditions. For a developer considering how to improve an intervention, the specific conditions under which it appeared to work or not work is the critical information to have. For a school system decision maker, the most useful pieces of information are insight into subpopulations that appear to benefit and conditions that are favorable for implementation. For those concerned with educational policy, it is often the case that conditions and interventions change and develop more rapidly than research studies can be conducted. Using available evidence may mean digging through studies that have confirmatory results in contexts similar or different from their own and examining exploratory analyses that provide useful hints as to the most productive steps to take next. The practitioner in this case is in a similar position to the researcher considering the design of the next experiment. The practitioner also has to come to a hypothesis about how things work as the basis for action.

Exploration in the World of Experimental Evaluation

Our 300+ page report makes a good start. But IES, faced with limited time and resources to complete the many experiments being conducted within the Regional Education Lab system, put strict limits on the number of exploratory analyses researchers could conduct. We usually think of exploratory work as questions to follow up on puzzling or unanticipated results. However, in the case of the REL experiments, IES asked researchers to focus on a narrow set of “confirmatory” results and anything else was considered “exploratory,” even if the question was included in the original research design.

The strict IES criteria were based on the principle that when a researcher is using tests of statistical significance, the probability of erroneously concluding that there is an impact when there isn’t one increases with the frequency of the tests. In our evaluation of AMSTI, we limited ourselves to only four such “confirmatory” (i.e., not exploratory) tests of statistical significance. These were used to assess whether there was an effect on student outcomes for math problem-solving and for science, and the amount of time teachers spent on “active learning” practices in math and in science. (Technically, IES considered this two sets of two, since two were the primary student outcomes and two were the intermediate teacher outcomes.) The threshold for significance was made more stringent to keep the probability of falsely concluding that there was a difference for any of the outcomes at 5% (often expressed as p < .05).

While the logic for limiting the number of confirmatory outcomes is based on technical arguments about adjustments for multiple comparisons, the limit on the amount of exploratory work was based more on resource constraints. Researchers are notorious (and we don’t exempt ourselves) for finding more questions in any study than were originally asked. Curiosity-based exploration can indeed go on forever. In the case of our evaluation of AMSTI, however, there were a number of fundamental policy questions that were not answered either by the confirmatory or by the exploratory questions in our report. More research is needed.

Take the confirmatory finding that the program resulted in the equivalent of 28 days of additional math instruction (or technically an impact of 5% of a standard deviation). This is a testament to the hard work and ingenuity of the AMSTI team and the commitment of the school systems. From a state policy perspective, it gives a green light to continuing the initiative’s organic growth. But since all the schools in the experiment applied to join AMSTI, we don’t know what would happen if AMSTI were adopted as the state curriculum requiring schools with less interest to implement it. Our results do not generalize to that situation. Likewise, if another state with different levels of achievement or resources were to consider adopting it, we would say that our study gives good reason to try it but, to quote Lee Cronbach, a methodologist whose ideas increasingly resonate as we translate research into practice: “…positive results obtained with a new procedure for early education in one community warrant another community trying it. But instead of trusting that those results generalize, the next community needs its own local evaluation” (Cronbach, 1975, p. 125).

The explorations we conducted as part of the AMSTI evaluation did not take the usual form of deeper examinations of interesting or unexpected findings uncovered during the planned evaluation. All the reported explorations were questions posed in the original study plan. They were defined as exploratory either because they were considered of secondary interest, such as the outcome for reading, or because they were not a direct causal result of the randomization, such as the results for subgroups of students defined by different demographic categories. Nevertheless, exploration of such differences is important for understanding how and for whom AMSTI works. The overall effect, averaging across subgroups, may mask differences that are of critical importance for policy

Readers interested in the issue of subgroup differences can refer to Table 6.11. Once differences are found in groups defined in terms of individual student characteristics, our real exploration is just beginning. For example, can the difference be accounted for by other characteristics or combinations of characteristics? Is there something that differentiates the classes or schools that different students attend? Such questions begin to probe additional factors that can potentially be addressed in the program or its implementation. In any case, the report just released is not the “final report.” There is still a lot of work necessary to understand how any program of this sort can continue to be improved.

Looking Back 35 Years to Learn about Local Experiments

With the growing interest among federal agencies in building local capacity for research, we took another look at an article by Lee Cronbach published in 1975. We found it has a lot to say about conducting local experiments and implications for generalizability. Cronbach worked for much of his career at Empirical’s neighbor, Stanford University, and his work has had a direct and indirect influence on our thinking. Some may interpret Cronbach’s work as stating that randomized trials of educational interventions have no value because of the complexity of interactions between subjects, contexts, and the experimental treatment. In any particular context, these interactions are infinitely complex, forming a “hall of mirrors” (as he famously put it, p. 119), making experimental results—which at most can address a small number of lower-order interactions—irrelevant. We don’t read it that way. Rather, we see powerful insights as well as cautions for conducting the kinds of field experiments that are beginning to show promise for providing educators with useful evidence.

We presented these ideas at the Society for Research in Educational Effectiveness conference in March, building the presentation around a set of memorable quotes from the 1975 article. Here we highlight some of the main ideas.

Quote #1: “When we give proper weight to local conditions, any generalization is a working hypothesis, not a conclusion…positive results obtained with a new procedure for early education in one community warrant another community trying it. But instead of trusting that those results generalize, the next community needs its own local evaluation” (p. 125).

Practitioners are making decisions for their local jurisdiction. An experiment conducted elsewhere (including over many locales, where the results are averaged) provides a useful starting point, but not “proof” that it will or will not work in the same way locally. Experiments give us a working hypothesis concerning an effect, but it has to be tested against local conditions at the appropriate scale of implementation. This brings to mind California’s experience with class size reduction following the famous experiment in Tennessee, and how the working hypothesis corroborated through the experiment did not transfer to a different context. We also see applicability of Cronbach’s ideas in the Investing in Innovation (i3) program, where initial evidence is being taken as a warrant to scale-up intervention, but where the grants included funding for research under new conditions where implementation may head in unanticipated directions, leading to new effects.

Quote #2: “Instead of making generalization the ruling consideration in our research, I suggest that we reverse our priorities. An observer collecting data in one particular situation…will give attention to whatever variables were controlled, but he will give equally careful attention to uncontrolled conditions…. As results accumulate, a person who seeks understanding will do his best to trace how the uncontrolled factors could have caused local departures from the modal effect. That is, generalization comes late, and the exception is taken as seriously as the rule” (pp. 124-125).

Finding or even seeking out conditions that lead to variation in the treatment effect facilitates external validity, as we build an account of the variation. This should not be seen as a threat to generalizability because an estimate of average impact is not robust across conditions. We should spend some time looking at the ways that the intervention interacts differently with local characteristics, in order to determine which factors account for heterogeneity in the impact and which ones do not. Though this activity is exploratory and not necessarily anticipated in the design, it provides the basis for understanding how the treatment plays out, and why its effect may not be constant across settings. Over time, generalizations can emerge, as we compile an account of the different ways in which the treatment is realized and the conditions that suppress or accentuate its effects.

Quote #3: “Generalizations decay” (p. 122).

In the social policy arena, and especially with the rapid development of technologies, we can’t expect interventions to stay constant. And we certainly can’t expect the contexts of implementation to be the same over many years. The call for quicker turn-around in our studies is therefore necessary, not just because decision-makers need to act, but because any finding may have a short shelf life.

Cronbach, L. J. (1975). Beyond the two disciplines of scientifi­c psychology. American Psychologist, 116-127.

Conference Season 2011

Empirical researchers will again be on the road this conference season, and we’ve included a few new conference stops. Come meet our researchers as we discuss our work at the following events. If you will be present at any of these, please get in touch so we can schedule a time to speak with you, or come by to see us at our presentations.

NCES-MIS

This year, the NCES-MIS “Deep in the Heart of Data” Conference will offer more than 80 presentations, demonstrations, and workshops conducted by information system practitioners from federal, state, and local K-12 agencies.

Come by and say hello to one of our research managers, Joseph Townsend, who will be running Empirical Education’s table display at the Hilton Hotel in Austin, Texas from February 23-25th. Joe will be presenting interactive demonstrations of MeasureResults, which allows school district staff to conduct complete program evaluations online.

SREE

Attendees of this spring’s Society for Research on Educational Effectiveness (SREE) Conference, held in Washington, DC March 3-5, will have the opportunity to discuss questions of generalizability with Empirical Education’s Chief Scientist, Andrew Jaciw and President, Denis Newman at two poster sessions. The first poster, entitled External Validity in the Context of RCTs: Lessons from the Causal Explanatory Tradition applies insights from Lee Cronbach to current RCT practices. In the second poster, The Use of Moderator Effects for Drawing Generalized Causal Inferences, Jaciw addresses issues in multi-site experiments. They look forward to discussing these posters both online at the conference website and in person.

AEFP

We are pleased to announce that we will have our first showing this year at the Association for Education Finance and Policy (AEFP) Annual Conference. Join us in the afternoon on Friday, March 25th at the Grand Hyatt in Seattle, WA as Empirical’s research scientist, Valeriy Lazarev, presents a poster on Cost-benefit analysis of educational innovation using growth measures of student achievement.

AERA

We will again have a strong showing at the 2011 American Educational Research Association (AERA) Conference. Join us in festive New Orleans, April 8-12 for the final results on the efficacy of the PCI Reading Program, our qualitative findings from the first year of formative research on our MeasureResults online program evaluation tool, and more.

View our AERA presentation schedule for more details and a complete list of our participants.

SIIA

This year’s SIIA Ed Tech Industry Summit will take place in gorgeous San Francisco, just 45 minutes north of Empirical Education’s headquarters in the Silicon Valley. We invite you to schedule a meeting with us at the Palace Hotel from May 22-24.

i3 Request for Proposals Calls for New Approaches to Rigorous Evaluation

In the strongest indication yet that the new administration is serious about learning from its multi-billion-dollar experience, the draft notice for the Invest in Innovation (i3) grants sets out new requirements for research and evaluation. While it is not surprising that the U.S. Department of Education requires scientific evidence for programs asking for funds for expansion and scaling up, it is important to note that strong evidence is now being defined not just in terms of rigorous methods but also in terms of “studies that in total include enough of the range of participants and settings to support scaling up to the State, regional, or national level.” This requirement for generalizability is a major step toward sponsoring research that has value for practical decisions. Along the same lines, high quality evaluations are those that include implementation data and performance feedback.

The draft notice also includes recognition of an important research design: “interrupted time series.” While not acceptable under the current What Works Clearinghouse criteria, this method—essentially looking for a change in a series of measures taken before and after implementing a new program—has enormous practical application for schools systems with solid longitudinal data systems.

Finally, we notice that ED is requiring that all evaluators cooperate with broader national efforts to combine evidence from multiple sources and will provide technical assistance to evaluators to assure consistency among researchers. They want to be sure at the end of the process they have useful evidence about what worked, what didn’t, and why.